How does the energy of an electron change when the electron moves closer to the nucleus?
Why do electrons not fall into the nucleus?
- Page ID
- 1665
The picture of electrons "orbiting" the nucleus similar planets around the sun remains an enduring 1, not just in popular images of the atom merely also in the minds of many of us who know better. The proposal, first fabricated in 1913, that the centrifugal force of the revolving electron but exactly balances the attractive force of the nucleus (in analogy with the centrifugal forcefulness of the moon in its orbit exactly counteracting the pull of the World'due south gravity) is a overnice picture, but is but untenable.

Ane origin for this hypothesis that suggests this perspective is plausible is the similarity of the gravity and Coulombic interactions. The expression for the force of gravity between two masses (Newton's Law of gravity) is
\[F_{gravity} \propto \dfrac{m_1m_2}{r^2}\label{1}\]
with
- \(m_1\) and \(m_2\) representing the mass of object 1 and 2, respectively and
- \(r\) representing the distance between the objects centers
The expression for the Coulomb force between ii charged species is
\[F_{Coulomb} \propto \dfrac{q_1q_2}{r^ii}\label{2}\]
with
- \(q_1\) and \(q_2\) representing the charge of object 1 and 2, respectively and
- \(r\) representing the distance between the objects centers
Nevertheless, an electron, unlike a planet or a satellite, is electrically charged, and it has been known since the mid-19th century that an electrical charge that undergoes acceleration (changes velocity and direction) volition emit electromagnetic radiations, losing energy in the procedure. A revolving electron would transform the atom into a miniature radio station, the free energy output of which would exist at the cost of the potential energy of the electron; according to classical mechanics, the electron would simply spiral into the nucleus and the atom would collapse.
Quantum theory to the Rescue!
By the 1920's, it became articulate that a tiny object such every bit the electron cannot exist treated as a classical particle having a definite position and velocity. The best we can do is specify the probability of its manifesting itself at whatsoever point in space. If you had a magic camera that could take a sequence of pictures of the electron in the 1s orbital of a hydrogen atom, and could combine the resulting dots in a single paradigm, you lot would see something like this. Clearly, the electron is more probable to be establish the closer we move toward the nucleus.
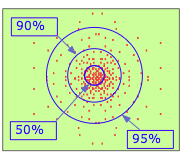
This is confirmed past this plot which shows the quantity of electron charge per unit volume of space at various distances from the nucleus. This is known equally a probability density plot. The per unit volume of space part is very of import here; as nosotros consider radii closer to the nucleus, these volumes become very small-scale, so the number of electrons per unit volume increases very quickly. In this view, it appears as if the electron does fall into the nucleus!
According to classical mechanics, the electron would simply spiral into the nucleus and the atom would collapse. Quantum mechanics is a different story.
The Boxing of the Infinities Saves the electron from its death spiral
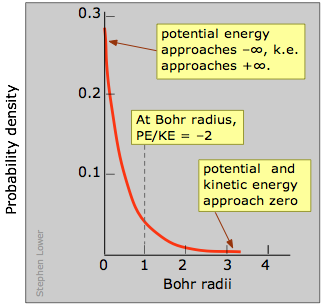
As you know, the potential energy of an electron becomes more than negative as information technology moves toward the attractive field of the nucleus; in fact, it approaches negative infinity. All the same, because the full energy remains constant (a hydrogen atom, sitting peacefully by itself, will neither lose nor learn energy), the loss in potential energy is compensated for by an increase in the electron's kinetic energy (sometimes referred to in this context as "confinement" energy) which determines its momentum and its constructive velocity.

So as the electron approaches the tiny volume of space occupied by the nucleus, its potential free energy dives downward toward minus-infinity, and its kinetic energy (momentum and velocity) shoots up toward positive-infinity. This "battle of the infinities" cannot be won by either side, so a compromise is reached in which theory tells u.s.a. that the fall in potential energy is just twice the kinetic energy, and the electron dances at an average distance that corresponds to the Bohr radius.
In that location is yet one affair wrong with this movie; according to the Heisenberg incertitude principle (a better term would be "indeterminacy"), a particle every bit tiny as the electron cannot be regarded equally having either a definite location or momentum. The Heisenberg principle says that either the location or the momentum of a quantum particle such as the electron tin be known as precisely every bit desired, only every bit one of these quantities is specified more precisely, the value of the other becomes increasingly indeterminate. It is important to understand that this is not simply a matter of observational difficulty, but rather a fundamental property of nature.
What this means is that within the tiny confines of the atom, the electron cannot actually be regarded as a "particle" having a definite energy and location, and so it is somewhat misleading to talk nigh the electron "falling into" the nucleus.
Arthur Eddington, a famous physicist, once suggested, non entirely in jest, that a better clarification of the electron would be "wavicle"!
Probability Density vs. Radial probability
We tin can, however, talk well-nigh where the electron has the highest probability of manifesting itself— that is, where the maximum negative accuse volition be found.
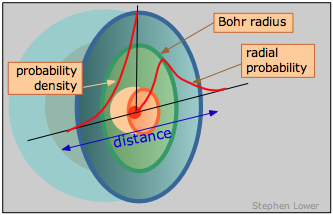
This is only the curve labeled "probability density"; its steep climb as we approach the nucleus shows unambiguously that the electron is near likely to be found in the tiny volume element at the nucleus. But expect! Did nosotros not just say that this does non happen? What nosotros are forgetting here is that every bit we move out from the nucleus, the number of these modest volume elements situated along any radius increases very speedily with \(r\), going upward by a factor of \(4πr^ii\). So the probability of finding the electron somewhere on a given radius circle is plant by multiplying the probability density past \(4πr^2\). This yields the bend yous have probably seen elsewhere, known as the radial probability, that is shown on the correct side of the above diagram. The peak of the radial probability for principal quantum number \(n = one\) corresponds to the Bohr radius.
To sum upward, the probability density and radial probability plots express two different things: the commencement shows the electron density at any unmarried point in the atom, while the second, which is generally more than useful to u.s., tells us the the relative electron density summed over all points on a circle of given radius.
References
- Why Doesn't the Electron Fall Into the Nucleus? Franklin Bricklayer and Robert Richardson, J Chem. Ed. 1983 (twoscore-42). Run across also the comment on this article past Werner Luck, J Chem Ed 1985 (914).
- For more detailed descriptions of these two kinds of plots, come across this McMaster U. page by Richard Bader.
- The author is grateful to Robert Harrison of U. of Tennessee-Knoxville whose suggestions led to improving this commodity.
Source: https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Quantum_Mechanics/09._The_Hydrogen_Atom/Atomic_Theory/Why_atoms_do_not_Collapse
Posted by: holtvared1955.blogspot.com


0 Response to "How does the energy of an electron change when the electron moves closer to the nucleus?"
Post a Comment